An fixed size "exponential" instance generator. More...
#include <generator.h>


Public Member Functions | |
| FSExponentialInstanceGenerator (int apps, int posts, double lambda) | |
| Create a new generator. More... | |
| FSExponentialInstanceGenerator (int apps, int posts, double lambda, int seed) | |
| Create a new generator. More... | |
| void | GenerateGML (std::ostream &o) |
| Generate a random structured instance in GML format. More... | |
| void | GenerateGraph (leda::graph &G, leda::list< leda::node > &A, leda::list< leda::node > &B, leda::node_map< int > &capacity, leda::edge_map< int > &rank) |
| Generate a random structured instance. More... | |
| int | NumPosts () const |
| int | NumApplicants () const |
Detailed Description
An fixed size "exponential" instance generator.
In several real-world assignment situations, the number of available positions (with capacities) is relatively low compared to the applicants. Moreover, there exists a total ordering 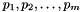 of the positions which is known in advance to all applicants (perhaps from an organization responsible for ranking the posts). Since people usually have a very strong opinion about their top choices and relatively weaker opinion about their last choices, this total ordering is strict at the beginning but allows equality towards the end. Based on this observation we divide posts into clusters of exponentially increasing size. These clusters are the same for all applicants. We maintain the following invariant. If an applicant assigns rank
of the positions which is known in advance to all applicants (perhaps from an organization responsible for ranking the posts). Since people usually have a very strong opinion about their top choices and relatively weaker opinion about their last choices, this total ordering is strict at the beginning but allows equality towards the end. Based on this observation we divide posts into clusters of exponentially increasing size. These clusters are the same for all applicants. We maintain the following invariant. If an applicant assigns rank 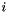 to a post of cluster
to a post of cluster 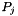 , then the applicant ranks all posts of the same cluster
, then the applicant ranks all posts of the same cluster 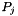 as rank
as rank 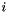 .
.
Not all applicants have the same self-confidence, translating to some applicants choosing to discart high choices completely, hoping to get an average one. We emulate this by assigning uniformly at random the first cluster that each applicant will rank. From then on the applicant ranks all remaining clusters.
Note that the last property of our generator can be justified by completely different examples as well. Suppose that a store wants to assign products to shelfs and we view the problem from the products viewpoint. All products want to be assigned to the best shelfs of the store. But not all products produce the same profit for the store-owner. Thus, the store owner is highly likely to restrict the accessibility of these selfs to a few products. Remaining products start biding from a lower quality shelf.
We use the following parameters: (a) number of applicants 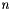 and number of posts
and number of posts 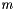 , and (b) a parameter
, and (b) a parameter 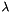 controlling the distribution of posts into clusters. More precisely, we construct clusters using the following strategy. We assign post
controlling the distribution of posts into clusters. More precisely, we construct clusters using the following strategy. We assign post 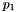 to the first cluster. Then for each post
to the first cluster. Then for each post 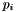 we choose with probability
we choose with probability 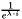 to construct a new cluster. Otherwise, we assign post
to construct a new cluster. Otherwise, we assign post 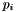 to the last constructed cluster. After the cluster construction each applicant chooses uniformly at random the first cluster to rank.
to the last constructed cluster. After the cluster construction each applicant chooses uniformly at random the first cluster to rank.
Constructor & Destructor Documentation
|
inline |
Create a new generator.
- Parameters
-
apps Number of applicants 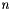 .
. posts Number of posts 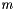 .
. lambda Parameter 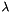
|
inline |
Create a new generator.
- Parameters
-
apps Number of applicants 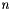 .
. posts Number of posts 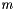 .
. lambda Parameter 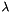
seed A seed for the random number generator
Member Function Documentation
|
inherited |
Generate a random structured instance in GML format.
- Parameters
-
o Output the GML graph in this stream
|
inherited |
Generate a random structured instance.
- Parameters
-
G The graph to return A The list of applicants B The list of posts capacity The node capacities rank The edge ranks
|
inlineinherited |
Number of applicants that the resulting instance will have.
|
inlineinherited |
Number of posts that the resulting instance will have.
 1.8.11
1.8.11