A highly correlated instance generator. More...
#include <generator.h>
Public Member Functions | |
| HighlyCorrelatedInstanceGenerator (int apps, int posts, double Density, double TieProp, int capacity) | |
| Create a new generator. More... | |
| HighlyCorrelatedInstanceGenerator (int apps, int posts, double Density, double TieProp, int capacity, int seed) | |
| Create a new generator. More... | |
| void | GenerateGML (std::ostream &o) |
| Generate a random structured instance in GML format. More... | |
| void | GenerateGraph (leda::graph &G, leda::list< leda::node > &A, leda::list< leda::node > &B, leda::node_map< int > &capacity, leda::edge_map< int > &rank) |
| Generate a random structured instance. More... | |
| int | NumPosts () const |
| int | NumApplicants () const |
Detailed Description
A highly correlated instance generator.
Highly correlated instances are problem instances where most of the applicants have a global and consistent knowledge of the posts reputation. Posts are already ranked, from an outside source, in some particular order 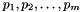 . This particular ranking is well known to all applicants and is gradly accepted, perhaps with a few minor adjustments per applicant. The goal is to have preferences which are based on the intuition that if two posts
. This particular ranking is well known to all applicants and is gradly accepted, perhaps with a few minor adjustments per applicant. The goal is to have preferences which are based on the intuition that if two posts 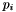 and
and 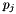 are far in the global ranking from each other then it should be highly likely that they are far away in each applicant's ranking as well.
are far in the global ranking from each other then it should be highly likely that they are far away in each applicant's ranking as well.
We model such instances based on the following parameters:
- number of applicants
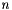 ,
, - number of posts
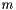 ,
, - a probability
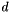 than an edge exists in our instance,
than an edge exists in our instance, - a probability
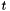 that an edge is tied to its predecessor, and
that an edge is tied to its predecessor, and - capacity
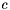 for all posts.
for all posts.
We create the instance in the following way. For each applicant 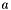 we randomly sample with probability
we randomly sample with probability 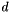 all posts, resulting in a subset
all posts, resulting in a subset 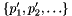 . We sort this subset of posts based on the total order
. We sort this subset of posts based on the total order 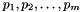 . For each post
. For each post 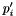 we create an edge
we create an edge 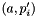 . We assign ranks as follows. We begin by giving edge
. We assign ranks as follows. We begin by giving edge 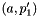 rank 1 and then we choose with probability
rank 1 and then we choose with probability 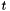 whether to assign edge
whether to assign edge 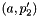 the same rank as
the same rank as 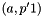 or to increase it. We continue this process for all remaining edges.
or to increase it. We continue this process for all remaining edges.
We call them highly correlated since preferences are highly related among applicants. These instances are particularly difficult with respect to popular matchings.
Constructor & Destructor Documentation
|
inline |
Create a new generator.
- Parameters
-
apps Number of applicants 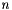 .
. posts Number of posts 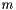 .
. Density Density parameter 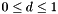
TieProp Tie probability 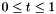
capacity Posts capacity 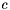
|
inline |
Create a new generator.
- Parameters
-
apps Number of applicants 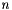
posts Number of posts 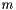
Density Density parameter 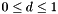
TieProp Tie probability 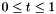
capacity Posts capacity 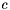
seed Seed value for the random number generator
Member Function Documentation
|
inherited |
Generate a random structured instance in GML format.
- Parameters
-
o Output the GML graph in this stream
|
inherited |
Generate a random structured instance.
- Parameters
-
G The graph to return A The list of applicants B The list of posts capacity The node capacities rank The edge ranks
|
inlineinherited |
Number of applicants that the resulting instance will have.
|
inlineinherited |
Number of posts that the resulting instance will have.
 1.8.11
1.8.11