Regional instance generator. More...
#include <generator.h>
Public Member Functions | |
| RegionalInstanceGenerator (int apps, int posts, int capacity, int regions, double lambda) | |
| Create a new generator. More... | |
| RegionalInstanceGenerator (int apps, int posts, int capacity, int regions, double lambda, int seed) | |
| Create a new generator. More... | |
| void | GenerateGML (std::ostream &o) |
| Generate a random structured instance in GML format. More... | |
| void | GenerateGraph (leda::graph &G, leda::list< leda::node > &A, leda::list< leda::node > &B, leda::node_map< int > &capacity, leda::edge_map< int > &rank) |
| Generate a random structured instance. More... | |
| int | NumPosts () const |
| int | NumApplicants () const |
Detailed Description
Regional instance generator.
Regional instances are best described using as example the assignment of students to universities. The generator tries to capture preferences which are a mixture of (a) a global and well accepted ranking of available posts and (b) stricty personal and emotional choices.
We assume that our instance has a number of regions 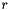 which is given as a parameter. The
which is given as a parameter. The 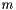 posts are divided roughly equally into the regions, thus, each region has
posts are divided roughly equally into the regions, thus, each region has 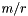 posts except possibly the last. Each post has a maximum capacity denoted by
posts except possibly the last. Each post has a maximum capacity denoted by 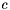 . Let
. Let 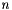 denote the number of applicants and let
denote the number of applicants and let 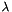 be a parameter which will affect the various distributions.
be a parameter which will affect the various distributions.
The regions are sorted in order of preference. We assume that this ordering is valid for all applicants (based for example on some global ranking) except for one region for each applicant. The exception is the region that each applicant belongs to. We assign applicants to regions uniformly at random. Let the ordering of the regions be 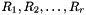 . Inside each region, posts are partitioned into clusters of exponentially increasing size. For region
. Inside each region, posts are partitioned into clusters of exponentially increasing size. For region 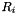 we denote as
we denote as 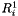 the set of best posts,
the set of best posts, 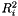 the second best and so on. This distribution is based on the parameter
the second best and so on. This distribution is based on the parameter 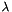 , in a similar fashion as in the other generators .
, in a similar fashion as in the other generators .
Let us now consider an applicant which belongs to region 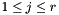 . The following matrix shows the rank of edges between the applicant and the set of employers
. The following matrix shows the rank of edges between the applicant and the set of employers 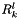 .
.
![\[ \begin{array}{c|c|c|c|c|c} & R^1 & R^2 & R^3 & R^4 & \ldots\\ \hline R_1 & 1 & 3 & 6 & 10 & \\ \hline R_j & 2 & 5 & 9 & & \\ \hline R_2 & 4 & 8 & & & \\ \hline R_3 & 7 & & & & \\ \hline \vdots& & & & & \ddots \\ \end{array} \]](form_46.png)
In other words each applicant tries to balance between the global ranking of the regions, her/his local region and the ranking of the clusters inside each region.
Constructor & Destructor Documentation
|
inline |
Create a new generator.
- Parameters
-
apps Number of applicants 
posts Number of posts 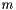
capacity Capacity of each post 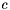
regions Number of regions 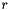
lambda Parameter for exponential ordering 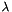
|
inline |
Create a new generator.
- Parameters
-
apps Number of applicants 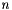
posts Number of posts 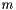
capacity Capacity of each post 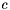
regions Number of regions 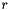
lambda Parameter for exponential ordering 
seed Seed value for the random number generator
Member Function Documentation
|
inherited |
Generate a random structured instance in GML format.
- Parameters
-
o Output the GML graph in this stream
|
inherited |
Generate a random structured instance.
- Parameters
-
G The graph to return A The list of applicants B The list of posts capacity The node capacities rank The edge ranks
|
inlineinherited |
Number of applicants that the resulting instance will have.
|
inlineinherited |
Number of posts that the resulting instance will have.
 1.8.11
1.8.11