An edge numbering class. More...

#include <edge_num.h>

Public Member Functions
	edge_num ()

	edge_num (const leda::graph &G)

	edge_num (const edge_num &)

	~edge_num (void)

edge_num &	operator= (const edge_num &)

int	operator() (leda::edge e) const

leda::edge	operator() (int i) const

bool	tree (leda::edge e) const

int	dim_cycle_space () const

int	num_weak_connected_comp () const

Detailed Description

An edge numbering class.

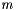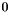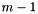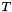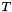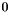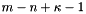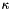This class assigns a unique numbering to the edges of a graph. The $m$ graph edges are numbered from $0$ to $m-1$ . The numbering is based on an arbitrary spanning tree $T$ . Edges not in $T$ are numbered from $0$ to $m -n + \kappa -1$ where $\kappa$ are the number of (weakly) connected components of 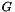$G$ . Edges in 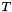$T$ are numbered from 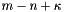$m-n+\kappa$ to $m-1$ .

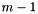An edge numbering is implemented as two arrays, and therefore requires 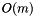$O(m)$ space. All operations take constant time except construction which takes linear time.

This is a static data structure. Changes in the graph after initializing an edge numbering invalidate the data structure.

Date: 2004-2005

Author: Dimitrios Michail

Constructor & Destructor Documentation

mcb::edge_num::edge_num ( )

Construct an edge numbering for the empty graph.

mcb::edge_num::edge_num ( const leda::graph & G )

explicit

Construct an edge numbering for a graph.

Parameters

G	The graph to construct for.

mcb::edge_num::edge_num ( const edge_num & )

Copy constructor

mcb::edge_num::~edge_num ( void )

Destructor

Member Function Documentation

int mcb::edge_num::dim_cycle_space ( ) const

inline

Get the dimension of the cycle space of 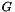$G$ . More precisely 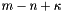$m - n + \kappa$ , where 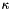$\kappa$ is the number of (weakly) connected components of the graph.

Returns: The dimension of the cycle space of the graph.

Referenced by mcb::cycle_matrix(), mcb::determinant(), and mcb::DMCB().

int mcb::edge_num::num_weak_connected_comp ( ) const

inline

Returns the number of (weakly) connected components of the graph.

Returns: The number of (weakly) connected components of the graph.

int mcb::edge_num::operator() ( leda::edge e ) const

inline

Access the number of an edge.

Parameters

e	The edge to access.

Returns: The unique number of the edge.

leda::edge mcb::edge_num::operator() ( int i ) const

inline

Access the edge with a particular number.

Parameters

i	An integer from 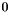to .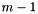

Returns: The edge corresponding to that integer.

edge_num& mcb::edge_num::operator= ( const edge_num & )

Assignment operator

bool mcb::edge_num::tree ( leda::edge e ) const

inline

Check if an edge belongs to the spanning forest used to construct the numbering.

Parameters

e An edge.

Returns: True if e belongs to the spanning forest, false otherwise.

Public Member Functions

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation