Undirected Minimum Cycle Basis | |
The functions below are the more general implementation for undirected graphs. They also support multigraphs. As an underlying implementation they use the Support Vector approach (mcb::UMCB_SVA). They should be the first choice of use unless some special requirements exist. | |
| template<class Container > | |
| int | mcb::UMCB_SVA (const graph &g, array< Container > &mcb, array< Container > &proof, const mcb::edge_num &enumb) |
| Compute a MCB of an undirected graph using the Support Vector Approach (de Pina's PhD thesis) algorithm. More... | |
| template<class Container > | |
| int | mcb::UMCB_SVA (const graph &g, array< Container > &mcb, const mcb::edge_num &enumb) |
| Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm. More... | |
| template<class W , class Container > | |
| W | mcb::UMCB_SVA (const graph &g, const edge_array< W > &len, array< Container > &mcb, array< Container > &proof, const mcb::edge_num &enumb) |
| Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm. More... | |
| template<class W , class Container > | |
| W | mcb::UMCB_SVA (const graph &g, const edge_array< W > &len, array< Container > &mcb, const mcb::edge_num &enumb) |
| Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm. More... | |
| int | mcb::UMCB_HYBRID (const leda::graph &g, leda::array< leda::d_int_set > &mcb, leda::array< leda::d_int_set > &proof, const mcb::edge_num &enumb) |
| Compute a minimum cycle basis of an undirected graph using a hybrid algorithm. More... | |
| int | mcb::UMCB_HYBRID (const leda::graph &g, leda::array< leda::d_int_set > &mcb, const mcb::edge_num &enumb) |
| Compute a minimum cycle basis of an undirected graph using a hybrid algorithm. More... | |
| template<class W > | |
| W | mcb::UMCB_HYBRID (const graph &g, const edge_array< W > &len, array< d_int_set > &mcb, array< d_int_set > &proof, const mcb::edge_num &enumb) |
| Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm. More... | |
| template<class W > | |
| W | mcb::UMCB_HYBRID (const graph &g, const edge_array< W > &len, array< d_int_set > &mcb, const mcb::edge_num &enumb) |
| Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm. More... | |
| template<class W > | |
| W | mcb::UMCB_FH (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, array< mcb::spvecgf2 > &proof, const mcb::edge_num &enumb) |
| Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm. More... | |
| template<class W > | |
| W | mcb::UMCB_FH (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm. More... | |
| template<class W > | |
| W | mcb::UMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library. More... | |
| int | mcb::UMCB (const graph &g, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library. More... | |
Directed Minimum Cycle Basis | |
| template<class W > | |
| W | mcb::DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, array< mcb::spvecfp > &proof, const mcb::edge_num &enumb, double error=0.375) |
| Compute a minimum cycle basis of a weighted directed graph. More... | |
| template<class W > | |
| W | mcb::DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| Compute a minimum cycle basis of a weighted directed graph. More... | |
| template<class W > | |
| W | mcb::DMCB (const graph &g, const edge_array< W > &len, array< array< etype > > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| Compute a minimum cycle basis of a weighted directed graph. More... | |
Detailed Description
Function Documentation
| W mcb::DMCB | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< mcb::spvecfp > & | mcb, | ||
| array< mcb::spvecfp > & | proof, | ||
| const mcb::edge_num & | enumb, | ||
| double | error = 0.375 |
||
| ) |
Compute a minimum cycle basis of a weighted directed graph.
The function computes a directed Minimum Cycle Basis 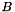 of
of  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of sparse vectors spvecfp, called mcb.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of sparse vectors spvecfp, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function also returns a certificate of optimality of the minimum cycle basis. More precisely a set of linearly independent vectors for which cycle 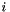 is the shortest cycle in
is the shortest cycle in  with non-zero intersection with the proof vector
with non-zero intersection with the proof vector 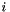 .
.
Since the algorithm is a randomized Monte-Carlo algorithm, the error argument which should be less that 1 represents the acceptable error probability that the returned cycle basis is not a minimum cycle basis.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 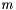 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g A directed graph. len The edge lengths. mcb A leda::array of spvecfp to return the MCB. proof A leda::array of spvecfp to return the proof. enumb An edge numbering. error The error probability.
- Precondition
- g is simple and loop-free
- len is positive
- enumb is already initialized with g
- error is positive and less than one
References mcb::edge_num::dim_cycle_space().
| W mcb::DMCB | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< mcb::spvecfp > & | mcb, | ||
| const mcb::edge_num & | enumb, | ||
| double | error = 0.375 |
||
| ) |
Compute a minimum cycle basis of a weighted directed graph.
The function computes a directed Minimum Cycle Basis 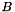 of
of  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of sparse vectors spvecfp, called mcb.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of sparse vectors spvecfp, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
Since the algorithm is a randomized Monte-Carlo algorithm, the error argument which should be less that 1 represents the acceptable error probability that the returned cycle basis is not a minimum cycle basis.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 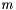 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g A directed graph. len The edge lengths. mcb A leda::array of spvecfp to return the MCB. enumb An edge numbering. error The error probability.
- Precondition
- g is simple and loop-free
- len is positive
- enumb is already initialized with g
- error is positive and less than one
| W mcb::DMCB | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< array< etype > > & | mcb, | ||
| const mcb::edge_num & | enumb, | ||
| double | error = 0.375 |
||
| ) |
Compute a minimum cycle basis of a weighted directed graph.
The function computes a directed Minimum Cycle Basis 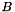 of
of  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of arrays of integers. Each such array if indexed on
with the smallest length (sum of lengths of cycles). The basis is returned as an array of arrays of integers. Each such array if indexed on  and its entry can be
and its entry can be 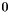 or
or 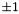 . Which edge corresponds to which index in this array can be found by the edge numbering, enumb. Note that the edge numbering using an indexing from
. Which edge corresponds to which index in this array can be found by the edge numbering, enumb. Note that the edge numbering using an indexing from 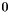 to
to 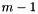 .
.
Since the algorithm is a randomized Monte-Carlo algorithm, the error argument which should be less that 1 represents the acceptable error probability that the returned cycle basis is not a minimum cycle basis.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 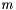 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g A directed graph. len The edge lengths. mcb A leda::array of leda::arrays of ints to return the MCB. enumb An edge numbering. error The error probability.
- Precondition
- g is simple and loop-free
- len is positive
- enumb is already initialized with g
- error is positive and less than one
References mcb::edge_num::dim_cycle_space().
| W mcb::UMCB | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< mcb::spvecgf2 > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library.
The function computes a Minimum Cycle Basis 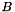 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of mcb:spvecgf2 objects.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of mcb:spvecgf2 objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 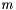 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. len The edge lengths function. mcb A leda::array of mcb::spvecgf2 to return the MCB. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| int mcb::UMCB | ( | const graph & | g, |
| array< mcb::spvecgf2 > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute an MCB of an undirected graph (possible a multigraph) using the most general implementation of this library.
The function computes a Minimum Cycle Basis 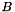 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of mcb:spvecgf2 objects.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of mcb:spvecgf2 objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 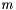 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. mcb A leda::array of mcb::spvecgf2 to return the MCB. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| W mcb::UMCB_FH | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< mcb::spvecgf2 > & | mcb, | ||
| array< mcb::spvecgf2 > & | proof, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm.
The function computes a Minimum Cycle Basis 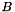 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). It accepts the length type as a template parameter. The basis is returned as an array of mcb::spvecgf2 objects.
with the smallest length (sum of lengths of cycles). It accepts the length type as a template parameter. The basis is returned as an array of mcb::spvecgf2 objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb. The function also returns a certificate of optimality of the minimum cycle basis. More precisely a set of linearly independent vectors for which cycle 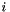 is the shortest cycle in
is the shortest cycle in  with odd intersection with the proof vector
with odd intersection with the proof vector 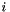 .
.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 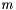 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. len A leda::edge_array for the edge lengths. mcb A leda::array of mcb::spvecgf2 to return the MCB. proof A leda::array of mcb::spvecgf2 to return the proof. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree.
- len is non-negative
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| W mcb::UMCB_FH | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< mcb::spvecgf2 > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a MCB of an undirected weighted graph using a Fast variant of the Hybrid algorithm.
The function computes a Minimum Cycle Basis 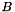 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). It accepts the length type as a template parameter. The basis is returned as an array of mcb::spvecgf2 objects.
with the smallest length (sum of lengths of cycles). It accepts the length type as a template parameter. The basis is returned as an array of mcb::spvecgf2 objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 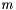 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. len A leda::edge_array for the edge lengths. mcb A leda::array of mcb::spvecgf2 to return the MCB. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree.
- len is non-negative
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| int mcb::UMCB_HYBRID | ( | const leda::graph & | g, |
| leda::array< leda::d_int_set > & | mcb, | ||
| leda::array< leda::d_int_set > & | proof, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a minimum cycle basis of an undirected graph using a hybrid algorithm.
The function computes a minimum cycle basis of an undirected graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function also returns a certificate of optimality of the minimum cycle basis. More precisely a set of linearly independent vectors for which cycle 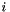 is the shortest cycle in
is the shortest cycle in  with odd intersection with the proof vector
with odd intersection with the proof vector 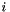 .
.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is 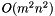 where
where 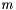 are the number of edges of
are the number of edges of  and
and 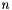 the number of vertices.
the number of vertices.
- Parameters
-
g An undirected graph. mcb A leda::array of leda::d_int_set to return the MCB. proof A leda::array of leda::d_int_set to return the proof. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree
Referenced by mcb::UMCB_HYBRID(), and mcb::UMCB_SVA().
| int mcb::UMCB_HYBRID | ( | const leda::graph & | g, |
| leda::array< leda::d_int_set > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a minimum cycle basis of an undirected graph using a hybrid algorithm.
The function computes a minimum cycle basis of an undirected graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is 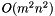 where
where 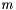 are the number of edges of
are the number of edges of  and
and 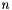 the number of vertices.
the number of vertices.
- Parameters
-
g An undirected graph. mcb A leda::array of leda::d_int_set to return the MCB. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree
| W mcb::UMCB_HYBRID | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< d_int_set > & | mcb, | ||
| array< d_int_set > & | proof, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm.
The function computes a minimum cycle basis of an undirected weighted graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function also returns a certificate of optimality of the minimum cycle basis. More precisely a set of linearly independent vectors for which cycle 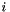 is the shortest cycle in
is the shortest cycle in  with odd intersection with the proof vector
with odd intersection with the proof vector 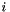 .
.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is 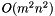 where
where 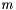 are the number of edges of
are the number of edges of  and
and 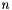 the number of vertices.
the number of vertices.
- Parameters
-
g An undirected graph. len A leda::edge_array for the edge lengths. mcb A leda::array of leda::d_int_set to return the MCB. proof A leda::array of leda::d_int_set to return the proof. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree
- len is non-negative
| W mcb::UMCB_HYBRID | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< d_int_set > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a minimum cycle basis of a weighted undirected graph using a hybrid algorithm.
The function computes a minimum cycle basis of an undirected weighted graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
with the smallest length (sum of lengths of cycles). The basis is returned as an array of dynamic integer sets, d_int_set, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is 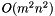 where
where 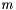 are the number of edges of
are the number of edges of  and
and 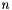 the number of vertices.
the number of vertices.
- Parameters
-
g An undirected graph. len A leda::edge_array for the edge lengths. mcb A leda::array of leda::d_int_set to return the MCB. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree
- len is non-negative
References mcb::UMCB_HYBRID().
| int mcb::UMCB_SVA | ( | const graph & | g, |
| array< Container > & | mcb, | ||
| array< Container > & | proof, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a MCB of an undirected graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
The function computes a Minimum Cycle Basis 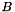 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). It accepts one template parameter which is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
with the smallest length (sum of lengths of cycles). It accepts one template parameter which is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb. The function also returns a certificate of optimality of the minimum cycle basis. More precisely a set of linearly independent vectors for which cycle 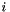 is the shortest cycle in
is the shortest cycle in  with odd intersection with the proof vector
with odd intersection with the proof vector 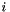 .
.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 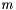 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. mcb A leda::array of Container to return the MCB. proof A leda::array of Container to return the proof. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree.
Referenced by mcb::UMCB_SVA().
| int mcb::UMCB_SVA | ( | const graph & | g, |
| array< Container > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
The function computes a Minimum Cycle Basis 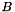 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). It accepts one template parameters which is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
with the smallest length (sum of lengths of cycles). It accepts one template parameters which is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 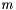 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. mcb A leda::array of Container to return the MCB. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree.
References mcb::UMCB_SVA().
| W mcb::UMCB_SVA | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< Container > & | mcb, | ||
| array< Container > & | proof, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
The function computes a Minimum Cycle Basis 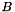 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). It accepts two template parameters. The first is length type and the second is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
with the smallest length (sum of lengths of cycles). It accepts two template parameters. The first is length type and the second is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb. The function also returns a certificate of optimality of the minimum cycle basis. More precisely a set of linearly independent vectors for which cycle 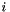 is the shortest cycle in
is the shortest cycle in  with odd intersection with the proof vector
with odd intersection with the proof vector 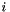 .
.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 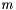 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. len A leda::edge_array for the edge lengths. mcb A leda::array of Container to return the MCB. proof A leda::array of Container to return the proof. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree.
- len is non-negative
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| W mcb::UMCB_SVA | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| array< Container > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute a MCB of an undirected weighted graph using the Support Vector Approach (de Pina's PhD thesis) algorithm.
The function computes a Minimum Cycle Basis 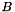 of a graph
of a graph  , that is a cycle basis of
, that is a cycle basis of  with the smallest length (sum of lengths of cycles). It accepts two template parameters. The first is length type and the second is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
with the smallest length (sum of lengths of cycles). It accepts two template parameters. The first is length type and the second is the container to use for recording the cycles. Currently two options are accepted, leda::d_int_set and mcb::spvecgf2. The basis is returned as an array of Container objects.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the Minimum Cycle Basis or is undefined if there were any errors.
The running time is  where
where 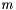 are the number of edges of
are the number of edges of  .
.
- Parameters
-
g An undirected graph. len A leda::edge_array for the edge lengths. mcb A leda::array of Container to return the MCB. enumb An edge numbering.
- Returns
- The length of the MCB or undefined if some error occured.
- Precondition
- g is undirected, simple and loopfree.
- len is non-negative
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
References mcb::UMCB_HYBRID().
 1.8.11
1.8.11