Introduction
A minimum cycle basis is a basis of the cycle space of a graph with minimum weight. The weight of a minimum cycle basis is the sum of the weights of its cycles and the weight of a cycle is the sum of the weights of its edges.
This package contains implementations of exact and approximate algorithms to compute minimum cycle bases for weighted directed and undirected graphs.
Algorithms
Undirected Graphs
- An
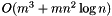 algorithm which appeared in the PhD thesis of J.C. de Pina. A description of this algorithm and an even faster one can be found here.
algorithm which appeared in the PhD thesis of J.C. de Pina. A description of this algorithm and an even faster one can be found here. - An
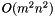 hybrid algorithm, which is a mixture of the above algorithm and an older algorithm due to Horton. For more details see here.
hybrid algorithm, which is a mixture of the above algorithm and an older algorithm due to Horton. For more details see here. - An
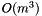 hybrid algorithm, which is a more clever implementation of the last mentioned algorithm. For more details see this paper.
hybrid algorithm, which is a more clever implementation of the last mentioned algorithm. For more details see this paper. - An
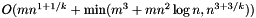 constant factor
constant factor 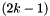 -approximate algorithm. For more details see this link.
-approximate algorithm. For more details see this link.
Directed Graphs
- An
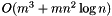 implementation of an
implementation of an 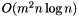 randomized Monte Carlo algorithm due to T. Kavitha, which appeared in ICALP'05.
randomized Monte Carlo algorithm due to T. Kavitha, which appeared in ICALP'05. - An
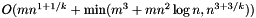 constant factor
constant factor 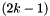 -approximate algorithm. For more details see this link.
-approximate algorithm. For more details see this link.
Requirements
This implementation is written in C++ and uses LEDA. The structure of the package follows that of a LEDA extension package (LEP).
Supported Platforms
Some versions of the package have been tested on the following platforms:
- gcc 3.x, 4.0.x and 4.1.x under Linux
- gcc 3.x under SunOS 5.9
- gcc 3.x under Cygwin
- bcc32 5.5 under Windows
- Visual Studio .NET 2003
but it may work on others too.
License
This program can be freely used in an academic environment
ONLY for research purposes, subject to the following restrictions:
1. The origin of this software must not be misrepresented; you must not
claim that you wrote the original software. If you use this software
an acknowledgment in the product documentation is required.
2. Altered source versions must be plainly marked as such, and must not be
misrepresented as being the original software.
3. This notice may not be removed or altered from any source distribution.
Any other use is strictly prohibited by the author, without an explicit
permission.
This software is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.Note that this package uses LEDA, which is not free. However, Algorithmic Solutions released a free version of LEDA 6.0 which can be used to build this library.
News
- 18 April 2008: v0.8 released
- LEDA 6.0 and LEDA 6.0 free support
- Interface change (not compatible with previous versions)
- A lot of improvements and new features.
- Improved demo program.
- 1 December 2006: v0.7 released
- Constant factor approximation algorithms for undirected and directed graphs.
- Interface change (not compatible with previous versions)
- 30 March 2006: v0.6 released
- Support for Microsoft VC++ 7.1 compiler.
- 27 Oct 2005: v0.5 released
- Speed improvements.
- Build system improvements.
- 30 June 2005: v0.4 released
- The code now is by default compiled with -O2 optimization flag.
- Minor fixes.
- 30 May 2005: v0.3 released
- Added algorithm for the directed case, still in BETA phase.
- Improved support for LEDA 5.0, including support on windows platform.
- 21 Mar 2005: v0.2 released
- minor changes in demo program.
- 24 Feb 2005: v0.1 released
Download
- Source package (v0.8). [tar.gz]
- Source package (v0.7). [tar.gz]
- Source package (v0.6). [tar.gz]
- Source package (v0.5). [tar.gz]
- Source package (v0.4). [tar.gz]
- Source package (v0.3). [tar.gz]
- Source package (v0.2). [tar.gz]
- Source package (v0.1). [tar.gz]
Source
The repository can be found at github.
 1.8.11
1.8.11