Undirected Approximate Minimum Cycle Basis | |
| template<class W > | |
| W | mcb::UMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| Compute an undirected approximate MCB of a weighted graph. More... | |
| int | mcb::UMCB_APPROX (const graph &g, const int k, array< mcb::spvecgf2 > &mcb, const mcb::edge_num &enumb) |
| Compute an undirected approximate MCB of a graph. More... | |
Directed Approximate Minimum Cycle Basis | |
| template<class W > | |
| W | mcb::DMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, double error=0.375) |
| Compute a directed approximate MCB of a weighted graph. More... | |
| template<class W > | |
| W | mcb::DMCB_APPROX (const graph &g, const edge_array< W > &len, const int k, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, mcb::ptype prime) |
Compute a directed approximate MCB of a weighted graph in 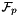 . Note that the minimum cycle basis in . Note that the minimum cycle basis in 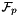 might not be the minimum cycle basis of the graph. More... might not be the minimum cycle basis of the graph. More... | |
Detailed Description
Function Documentation
| W mcb::DMCB_APPROX | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| const int | k, | ||
| array< mcb::spvecfp > & | mcb, | ||
| const mcb::edge_num & | enumb, | ||
| double | error = 0.375 |
||
| ) |
Compute a directed approximate MCB of a weighted graph.
The function computes an 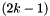 -approximate Minimum Cycle Basis
-approximate Minimum Cycle Basis 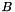 of a graph
of a graph 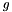 . The basis is returned as an array of sparse vectors, spvecfp, called mcb.
. The basis is returned as an array of sparse vectors, spvecfp, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
Since the algorithm is a randomized Monte-Carlo algorithm, the error argument which should be less that 1 represents the acceptable error probability that the returned cycle basis is not a 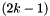 -approximate minimum cycle basis.
-approximate minimum cycle basis.
The function returns the weight of the approximate Minimum Cycle Basis or is undefined if there were any errors.
The running time is 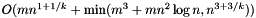 where
where 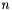 are the number of nodes of
are the number of nodes of 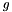 ,
, 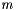 the number of edges and
the number of edges and 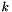 is an integer
is an integer 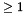 .
.
- Parameters
-
g An directed graph. len A leda::edge_array for the edge lengths. k How much to approximate? mcb A leda::array of spvecfp to return the approx MCB. enumb An edge numbering. error The error probability
- Returns
- The length of the approximate MCB or undefined if some error occured.
- Precondition
- g is loopfree.
- len is non-negative
- k must be an integer greater than zero
- error is positive and less than one
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| W mcb::DMCB_APPROX | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| const int | k, | ||
| array< mcb::spvecfp > & | mcb, | ||
| const mcb::edge_num & | enumb, | ||
| mcb::ptype | prime | ||
| ) |
Compute a directed approximate MCB of a weighted graph in 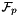 . Note that the minimum cycle basis in
. Note that the minimum cycle basis in 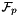 might not be the minimum cycle basis of the graph.
might not be the minimum cycle basis of the graph.
The basis is returned as an array of sparse vectors, spvecfp, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the possibly approximate Minimum Cycle Basis or is undefined if there were any errors.
The running time is 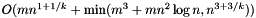 where
where 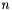 are the number of nodes of
are the number of nodes of 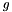 ,
, 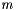 the number of edges and
the number of edges and 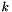 is an integer
is an integer 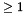 .
.
- Parameters
-
g An directed graph. len A leda::edge_array for the edge lengths. k How much to approximate? mcb A leda::array of spvecfp to return the approx MCB. enumb An edge numbering. prime A leda::integer prime number in order to do the computation in 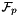 .
.
- Returns
- The length of the approximate MCB or undefined if some error occured.
- Precondition
- g is loopfree.
- len is non-negative
- k must be an integer greater than zero
- prime is a prime number > 2
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| W mcb::UMCB_APPROX | ( | const graph & | g, |
| const edge_array< W > & | len, | ||
| const int | k, | ||
| array< mcb::spvecgf2 > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute an undirected approximate MCB of a weighted graph.
The function computes an 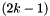 -approximate Minimum Cycle Basis
-approximate Minimum Cycle Basis 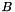 of a graph
of a graph 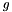 . The basis is returned as an array of sparse vectors, spvecgf2, called mcb.
. The basis is returned as an array of sparse vectors, spvecgf2, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the approximate Minimum Cycle Basis or is undefined if there were any errors.
Even if the graph is directed this function computes an approximate MCB of the underlying undirected graph.
The running time is 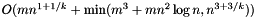 where
where 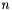 are the number of nodes of
are the number of nodes of 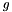 ,
, 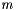 the number of edges and
the number of edges and 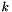 is an integer
is an integer 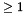 .
.
- Parameters
-
g An graph. len A leda::edge_array for the edge lengths. k How much to approximate? mcb A leda::array of spvecgf2 to return the MCB. enumb An edge numbering.
- Returns
- The length of the approximate MCB or undefined if some error occured.
- Precondition
- g is loopfree.
- len is non-negative
- k must be an integer greater than zero
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
| int mcb::UMCB_APPROX | ( | const graph & | g, |
| const int | k, | ||
| array< mcb::spvecgf2 > & | mcb, | ||
| const mcb::edge_num & | enumb | ||
| ) |
Compute an undirected approximate MCB of a graph.
The function computes an 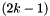 -approximate Minimum Cycle Basis
-approximate Minimum Cycle Basis 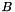 of a graph
of a graph 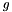 . The basis is returned as an array of sparse vectors, spvecgf2, called mcb.
. The basis is returned as an array of sparse vectors, spvecgf2, called mcb.
Every edge is represented by some integer, by a fixed and arbitrary numbering. This numbering is represented by enumb.
The function returns the weight of the approximate Minimum Cycle Basis or is undefined if there were any errors.
Even if the graph is directed this function computes an approximate MCB of the underlying undirected graph.
The running time is 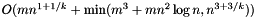 where
where 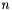 are the number of nodes of
are the number of nodes of 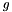 ,
, 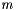 the number of edges and
the number of edges and 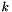 is an integer
is an integer 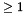 .
.
- Parameters
-
g An undirected graph. k How much to approximate? mcb A leda::array of spvecgf2 to return the MCB. enumb An edge numbering.
- Returns
- The length of the approximate MCB or undefined if some error occured.
- Precondition
- g is loopfree.
- len is non-negative
- k must be an integer greater than zero
- Remarks
- Care must be taken when the template parameter is instantiated with a data type which has rounding errors.
 1.8.11
1.8.11