Algorithms for directed MCB. More...

#include <LEP/mcb/config.h>
#include <LEDA/graph.h>
#include <LEDA/array.h>
#include <LEDA/edge_array.h>
#include <LEDA/integer.h>
#include <LEDA/random_source.h>
#include <LEP/mcb/edge_num.h>
#include <LEP/mcb/fp.h>
#include <LEP/mcb/spvecfp.h>
#include <LEP/mcb/arithm.h>
#include <LEP/mcb/transform.h>
#include <LEP/mcb/dsigned.h>

Include dependency graph for dmcb.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Namespaces
	mcb
	The main package namespace.

Functions
Directed Minimum Cycle Basis
template<class W >
W	mcb::DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, array< mcb::spvecfp > &proof, const mcb::edge_num &enumb, ptype &p)

template<class W >
W	mcb::DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, array< mcb::spvecfp > &proof, const mcb::edge_num &enumb, double error=0.375)
	Compute a minimum cycle basis of a weighted directed graph. More...

template<class W >
W	mcb::DMCB (const graph &g, const edge_array< W > &len, array< mcb::spvecfp > &mcb, const mcb::edge_num &enumb, double error=0.375)
	Compute a minimum cycle basis of a weighted directed graph. More...

template<class W >
W	mcb::DMCB (const graph &g, const edge_array< W > &len, array< array< etype > > &mcb, const mcb::edge_num &enumb, double error=0.375)
	Compute a minimum cycle basis of a weighted directed graph. More...

Detailed Description

Algorithms for directed MCB.

Given an directed graph 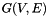$G(V,E)$ and a positive length function on the edges 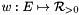$w: E \mapsto \mathcal{R}_{> 0}$ , a minimum cycle basis is a set of cycles which can generate the cycle space and at the same time has minimum total length.

Each cycle of the graph is assumed to be a vector in 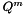$Q^m$ indexed on the edge set, and operations between cycles is performed in 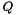$Q$ . The length of a cycle basis is the sum of the length of its cycles and the length of a cycle is the sum of the length of its edges.

Most functions of this section are templates functions. The template parameter W denoting the type of the edge weights can be instantiated with any number type. Attention must be paid in order to avoid overflow of values.

The solution of a minimum cycle basis problem can be in the following two forms.

A pair (mcb, proof) where both are arrays of mcb::spvecfp. A mcb::spvecfp is a wrapper around Leda's list datatype. Each element in this list, is a two_tuple<long,integer>, where the first argument is its index 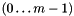$(0 \dots m-1)$ and the second is in case of mcb a value of 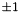${\pm}1$ where positive is an arbitrary direction of traversing the cycle and in case of proof a value in 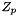for some prime number 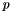. Each index represents an edge.
The number of an edge can be found by the edge numbering, edge_num.
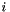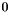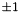A solution mcb which is an array of arrays of mcb::etype (currently short ints), array<mcb::etype>. Each element of this array represents a cycle of the minimum cycle basis. Each entry of the array is or ${\pm}1$ , based on whether the edge 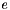with number 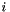( enumb(e) = i ) belongs to the cycle and if yes in which direction compared with an arbitrary direction of traversing the cycle.

The whole package is protected using a namespace called "mcb", and therefore using anything requires mcb::xx or the using namespace mcb directive.

See also: mcb::spvecfp

Namespaces

Functions

Detailed Description